Sort definition, a fundamental concept in data structures, plays a crucial role in organizing and managing data. From simple arrangements to complex computations, sorting algorithms form the backbone of efficient data processing.
This comprehensive guide delves into the intricacies of sorting, exploring its applications, algorithms, implementation, optimization, and impact on data analysis and decision-making.
Overview of Sort Definition
Sorting is a fundamental operation in data structures that involves arranging elements of an array or list in a specific order, typically ascending or descending. It plays a crucial role in data management and analysis, enabling efficient searching, retrieval, and processing of information.
Various sorting algorithms exist, each with its own time and space complexity characteristics. Some common sorting algorithms include:
- Bubble Sort
- Selection Sort
- Insertion Sort
- Merge Sort
- Quick Sort
- Heap Sort
Applications of Sorting
Sorting finds widespread applications in real-world scenarios, including:
- Data Retrieval:Sorting data enables efficient searching and retrieval of specific elements from large datasets.
- Data Analysis:Sorting allows for the analysis of data patterns, trends, and outliers, facilitating decision-making and problem-solving.
- Data Visualization:Sorting helps in organizing data for effective visualization, such as creating charts and graphs.
- Database Management:Sorting is essential for optimizing database queries and improving data access performance.
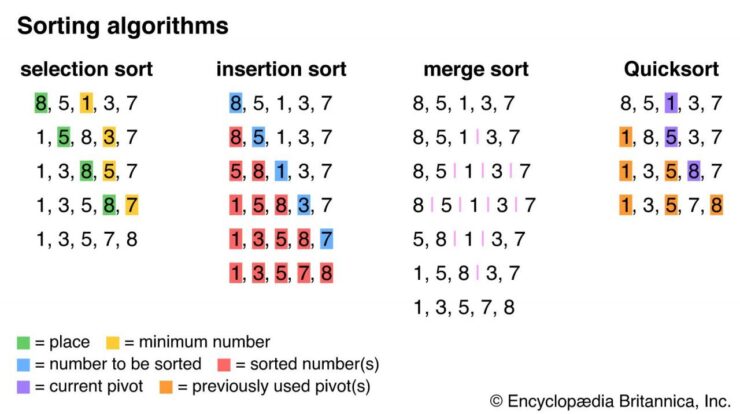
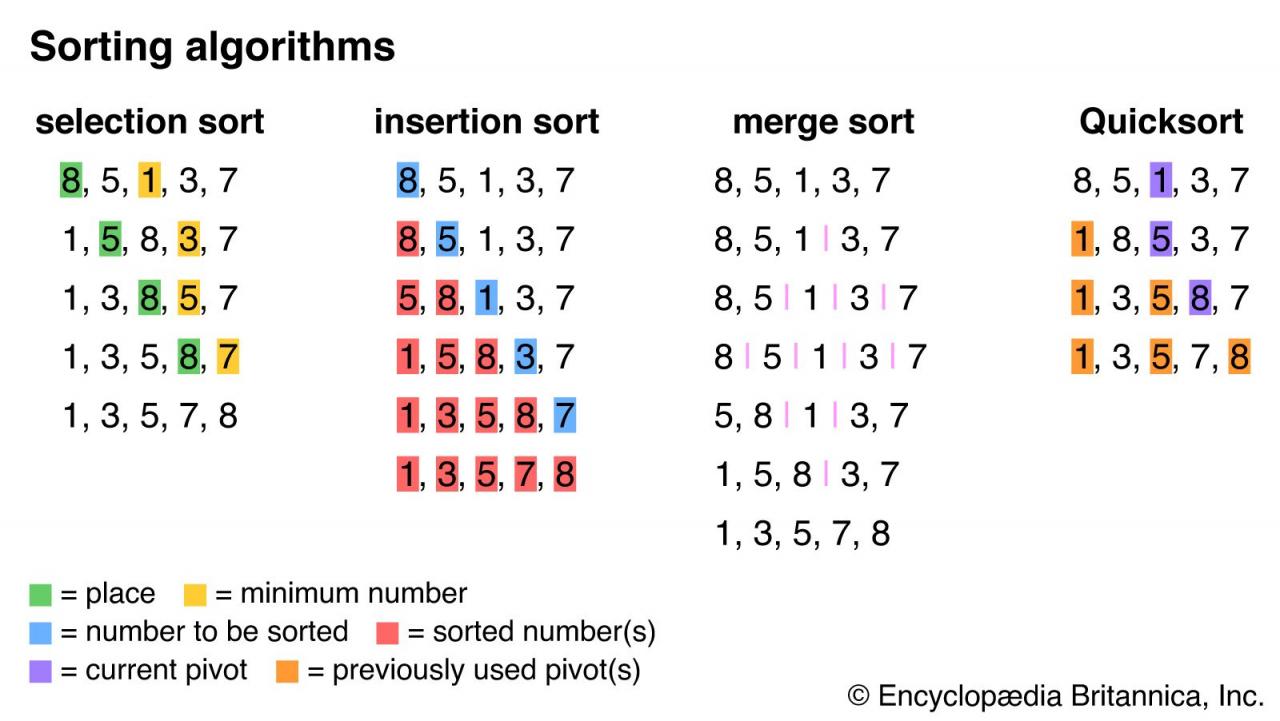
Sorting Algorithms
| Algorithm | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Bubble Sort | O(n^2) | O(1) | Compares adjacent elements and swaps them if they are in the wrong order. |
| Selection Sort | O(n^2) | O(1) | Finds the minimum element from the unsorted portion and swaps it with the leftmost unsorted element. |
| Insertion Sort | O(n^2) | O(1) | Inserts each element into its correct position in the sorted portion of the array. |
| Merge Sort | O(n log n) | O(n) | Divides the array into smaller subarrays, sorts them, and merges them back together. |
| Quick Sort | O(n log n) | O(log n) | Selects a pivot element, partitions the array into two subarrays, and sorts them recursively. |
| Heap Sort | O(n log n) | O(1) | Builds a heap data structure from the array and repeatedly extracts the maximum element. |
Implementation of Sorting Algorithms
Sorting algorithms can be implemented in various programming languages. Here’s an example of implementing Bubble Sort in Python:
def bubble_sort(arr):
"""
Bubble Sort implementation in Python.
Args:
arr (list): The list to be sorted.
Returns:
list: The sorted list.
"""
n = len(arr)
for i in range(n):
for j in range(0, n
- i
- 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
Optimization of Sorting Algorithms
Sorting algorithms can be optimized using various techniques, such as:
- Choosing the Right Algorithm:Selecting the appropriate sorting algorithm based on the data size and type can significantly improve performance.
- In-Place Sorting:Algorithms that sort the data in-place, without creating additional memory space, can be more efficient.
- Cutoff Threshold:Using a cutoff threshold to switch to a simpler sorting algorithm for small datasets can enhance efficiency.
- Hybrid Sorting:Combining different sorting algorithms to leverage their strengths can improve overall performance.
Last Point
In conclusion, sorting algorithms are indispensable tools for data manipulation, offering a wide range of techniques to organize and retrieve data efficiently. Understanding their complexities, applications, and optimization strategies empowers developers and data analysts to harness the full potential of sorted data, driving informed decision-making and unlocking valuable insights.
Essential FAQs: Sort Definition
What is the purpose of sorting?
Sorting organizes data in a specific order, making it easier to search, retrieve, and analyze.
Which sorting algorithm is the most efficient?
The efficiency of a sorting algorithm depends on the data set and the desired sorting order. Common efficient algorithms include QuickSort, MergeSort, and HeapSort.
How can I optimize sorting algorithms?
Optimization techniques include choosing the right algorithm for the data, reducing unnecessary comparisons, and implementing caching mechanisms.